

Ok here's the deal.
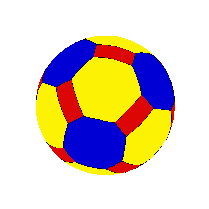
Let v=# vertices
Let e=# edges
Let f=# faces
At least for the polyhedra you can make in Kaleidotile,
Isn't that amazing?! This is called the Euler Characteristic of the Sphere.
Q3 Once you've done this, do you think this constant is the same
for non-convex (spiky) polyhedra? Conjecture and explain.


This constant is a topological property, not a geometric one:
Q4 Does the constant change as the surface is stretched and
distorted?
What is an appropriate definition of face, vertex and edge that applies
even after distortion?


In geometry, one is concerned with measurements like angles, lengths
and areas. In geometry a circle is defined as all points a fixed distance
from some fixed point and all lines are straight.
Topology is a closely related field, but is concerned more with
properties
that are preserved after arbitrary distortions, like whether two objects
touch. To a topologist, all those strange
little fellows we saw at the very beginning of the unit are completely
equivalent. All simple closed curves are equivalent to circles, and all
arcs that have no endpoints are equivalent to lines.
All of these objects are topologically disks:

The standard "joke" is that a topologist confuses her coffee
cup for the donut:
Topological properties are intrinsic: A flat-lander could
distinguish
between the mobius band and the other surfaces (because it has only one
edge, for example). But the first and third surfaces are topologically
equivalent:
both are made by taking a band and gluing opposite sides together
top-to-top
and bottom-to-bottom. A flat-lander could not tell any difference between
the two. The two surfaces are equivalent if one ignores how they are
actually
placed in our space.

When dealing with surfaces, this is a handy point of view, since we aren't concerned with the specific arrangement of the surface in our space.
Chaim Goodman-Strauss Dept. Mathematics Univ. Arkansas Fayetteville, AR 72701 strauss@comp.uark.edu 501-575-6332