Hmk IV: Before considering planar patterns, think
about circular and linear patterns in the plane. The circular
patterns are generated by dihedral and cyclic symmetries and have an infinite
wedge as their motif. Could there be any others?
The linear patterns are known as the freize groups and have as motif
either an infinite strip, or half of an infinite strip. The infinite cyclic
and dihedral symmetries are examples, as is the symmetry generated by a
single glide reflection. Examine the sketches *inf.inf,
inf.inf , inf* and inf.o ; in particular, how was each generated? How
do they differ? Can you think of any other linear symmetries? (Hint: try
a two-fold rotation on the edge of an infinite strip). There are seven total!
For one of your new symmetries, make a sketch similar to the ones given here.
Hmk V: Think of as many planar patterns-- infinite, regular repetition of a motif-- as you can. In particular, consider how some of the patterns in Rules of the game could be generalized. We're concerned with the ways this repetition can be caried out, not the appearance of the motif itself.
You might begin by considering the following:
1) How many ways a square could serve as a motif?(see Bonus Homework, for a good start!)
Try out different generating isometries and see what happens... See if you
can get at least 12 different planar patterns.
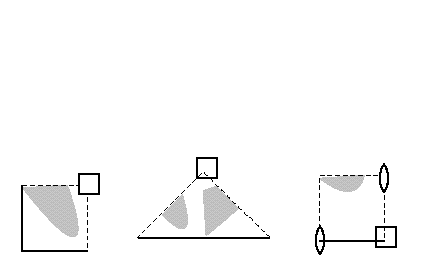
2) Are all these patterns different? For example, consider these three
generating motifs: (if you'd like, return to the
visual notation. 
3) How could you classify planar patterns?
These questions are really meant to set the stage for next week, when we analyze the general situation!
Chaim Goodman-Strauss Dept. Mathematics Univ. Arkansas Fayetteville, AR 72701 strauss@comp.uark.edu 501-575-6332