
Hyperbolic space is a fascinating placefull of surprises. But it can be easy to develop some good intuition:
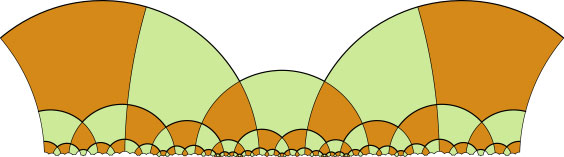
We'll begin with the claim that in the above picture, all the shapes are congruent! That is, somehow they are the same shape and size. Of course, we don't mean in the picture itself, but in the space the picture represents.
You've seen something like this before when you've looked at maps. Sizes have to be distorted on any map of the Earth. On many maps, for example, Greenland looks bigger than Africa even though it is in fact much much smaller! And Antartica appears larger than all the rest of the continents put together!
We have to distort sizes when we draw a picture of the sphere. Similarly, we have to distort sizes when we draw a picture of the hyperbolic plane.
Just as there are many different kinds of projections used to make maps of the Earth, there are many ways to draw pictures of the hyperbolic plane. The upper-half plane model is one particularly nice projection.
In any case, all the colored regions are exactly the same shape and size.
What properties would have to hold if indeed these are all to be congruent?
First let's make a few observations: each of the shapes is pentagonal, and is bounded by circles that meet the bottom of the picture at right angles. Second, these pentagons meet 4-to-a-vertex, and two circles meet at right angles at each vertex. Most importantly, note that "inversion" through any of these circles will take these pentagons to one another.
1: there is a special line (the x-axis). Let us call it the line at infinity, for reasons that will be clear soon.
2: there are special circles: those whose centers lie on the line at infinity. Let's call these geodesics. We'll see soon that these are actually straight paths in the geometry!
3: inversion through a geodesic is supposed to preserve distance.
Inversion reverses orientation and so should correspond to a reflection. But the curve we reflect across must be considered "straight": the two sides of the curve must be congruent and so the curve can't bend one way or the other. Consequently, taking as an axiom that inversion preserves distance and reverses orientation, our special circles really must be geodesics, or straight curves.
This may seem pretty strange. Here's another way to look at it: if all the pentagons are the same size, which path is shorter? The horizontal line crosses about a dozen pentagons; the geodesic follows only five!
Let's now go on to isometries.
Chaim Goodman-Strauss strauss@delojo.com