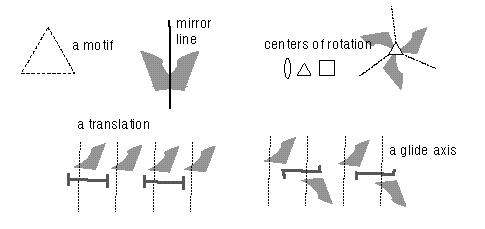
Patterns propogate simply by repeating the motif and the generators as pictured below. This always works-- if you get a conflict, the motif and generators were "illegal".
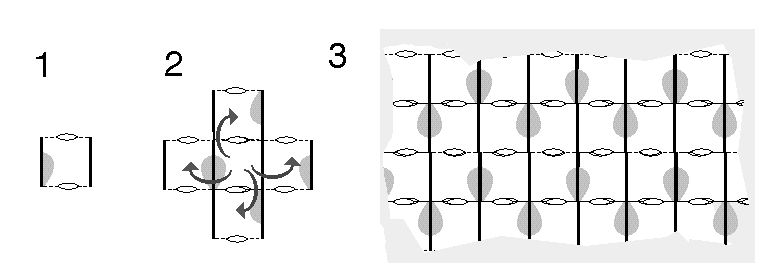
Q5: For example, what patterns are generated
by these motifs? Do any of these generate the same pattern? Do all
of these actually generate a pattern or do some lead to a violation of
the rules?
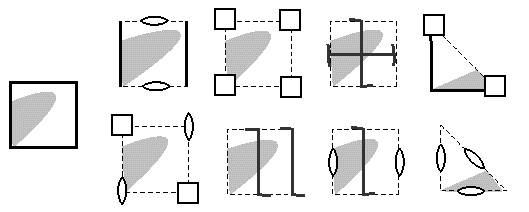
If our motif is repeated by congruences, we are applying a series of rotations, reflections and translations. We will examine a few more examples and then explore the general case. In time we must find out which combinations do not lead to trouble. Next, though, we'll apply our new notation and analyze some pix!
To theGallery
to outline
 Chaim Goodman-Strauss
Dept. Mathematics
Univ. Arkansas
Fayetteville, AR 72701
strauss@comp.uark.edu
501-575-6332
Chaim Goodman-Strauss
Dept. Mathematics
Univ. Arkansas
Fayetteville, AR 72701
strauss@comp.uark.edu
501-575-6332