Transactions AMS 349 (1997) 4429-4464
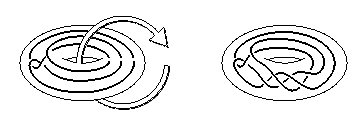
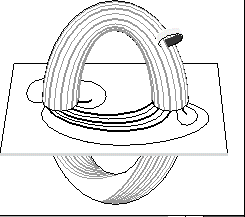
Here's a picture of a twisting of a knot:

If you'd like to see a "magic trick" involving this operation, just click. (Due to K. Motegi)
Y. Mathieu invented this twisting operation in 1989 or so, and asked which knots are related by twisting. A twisting of a knot K is parametrized by a choice of oriented twisting torus V and number of full twists d (=delta in paper). In 1991 Motegi conjectured that each presentation of K in V gives rise to at most one composite twisted unknot and that this composite knot arises from a single twist of K . In that paper he proved that the number of twists d must be less than six.
Miyazaki next gave a necessary condition for a composite knot to be a twisted unknot, ruling out, for example, the granny knot; about then Teragaito gave some especially amusing examples of composite twisted unknots.
In 1993 I proved the following theorems, adapting the techniques of John Luecke and Cameron Gordon:
1. If an unknot is given more than one full twist, the result is prime.
That is, if K is a composite twisted unknot, d=1.
2. If a composite knot is given three (non-trivial) full twists, the result is prime. If a composite knot is given two (non-trivial) full twists and the result is composite, we began with a granny knot and obtained the granny knot of opposite handedness.
The granny knot case is due to Motegi and Hayashi, and required very special attention in the proof (an additional strand had to be woven through the induction. From a very technical standpoint, this is the most interesting part of the paper.)
Corollary to 2. Thus, if twisting an unknot one full twist in one direction gives a composite knot, twisting one full twist in the other direction gives a prime knot. That is, given an unknot and twisting torus V, there's at most one twisting of V that gives a composite knot.
So much for negative results. Here are the positive results:
3 : If K is a composite twisted unknot such that d=1 and (*), then K in V(1) is of the form K =S(d) #-k_1 , where
(i) k is a torus 1-bridge knot with presentation in and on a solid
torus V';
(ii) -k_1 is the reflection of a (1,V')-twisting of k;
(iii) and S(k) is any restricted band sum with respect to V' of k with a
collection of disjoint (1,1) and (0,0) curves on the boundary of V' .
Furthermore, all knots K=S(k)#(-k_1) , as described, are indeed composite
twisted unknots.
(1-bridge torus knot and restricted band sum are defined in the paper)
where (*) is the condition that the intersection of the splitting sphere of K and the twisting torus V has two components. I give several examples that show that the techniques used so far break down completely, in several ways, when approaching (*). Since Theorem 1 assures d must equal 1, the classification is thus complete, up to this renegade hypothesis.
Corollary to 3 All known examples, although seeming quite different, are easily given a representation in the form outlined. The picture above is a graphical shorthand for one of Teragaito's examples, put in the form of Theorem 3.
4 Finally, for fun: Given any composite knot K and any (j,2) torus knot there are an infinite number of twisting tori around K that yield, after a single twist, a non-trivial composite knot with one summand the (j,2) torus knot.
Independently, Motegi and Hayashi proved Theorem 1; Teragaito proved a weaker version of Theorem 1; and Motegi and Hayashi proved the first sentence in Theorem 2 and gave the very amusing granny knot example mentioned in that theorem.