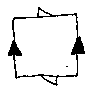

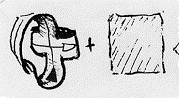
How can the Klein bottle be seen as a pair of bands sewn to a square disk along their single edge?
We begin by recalling that a Klein bottle can
be made from a square with its sides glued together in a particular way:



How can the Klein bottle be seen as a pair of bands sewn to a square disk
along their single edge?
Lets see:
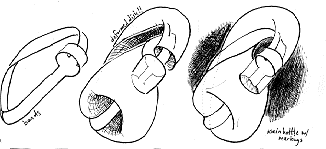
Here we see a Klein bottle drawn as the union of a pair of bands (Left)
and a disk (middle).

note this is the same as fattening the curves on the left on the klein bottle
when it is formed from a square.
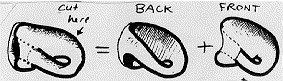
In the gluing-up-the-square diagram, these Mobius bands look like: 
Find this band in the Klein Bottle!
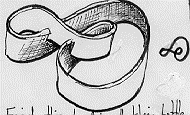
Is it one sided or two sided?
What are the remaining pieces of the Klein bottle when this band is removed?
Another thing:
After you cut a Mobius band down the middle, you can arrange the result
to look like the above! How many twists does this band have?
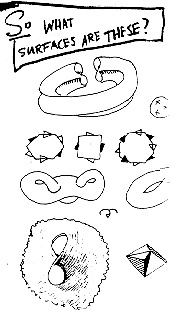
Extra Bonus: classify all surfaces!
Chaim Goodman-Strauss Dept. Mathematics Univ. Arkansas Fayetteville, AR 72701 cgstraus@comp.uark.edu 501-575-6332
(c)1992-1994 Chaim Goodman-Strauss
Clean paper masters available on request.