
The final case is that the two lines of reflection, l1 and l2, do not meet at all. The result of reflecting first across l1, then across l2, is a translation or hyperbolic transformation. These correspond, in some sense to translations in the Euclidean plane.
Click on the image to download an interactive demonstration. (To use the demonstrations, you must have Geometer's Sketchpad. A demo version is available here)
Parabolic transformations follow hypercycles: a family of curves passing through the same points at infinity. One special hypercycle in this family will be a geodesic.
Click on the image to download an interactive demonstration.
You can download a Quicktime animation of the following image, which shows points moving along a family of hypercycles by translations:
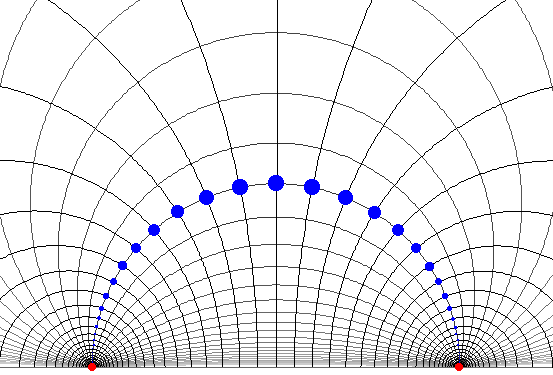
download the
large version (800K)
small version (200K)
(Be sure to set the movies to Loop in the Movie Menu in your Quicktime player)
Chaim Goodman-Strauss strauss@delojo.com